"Lõpmatusse ja edasi!"
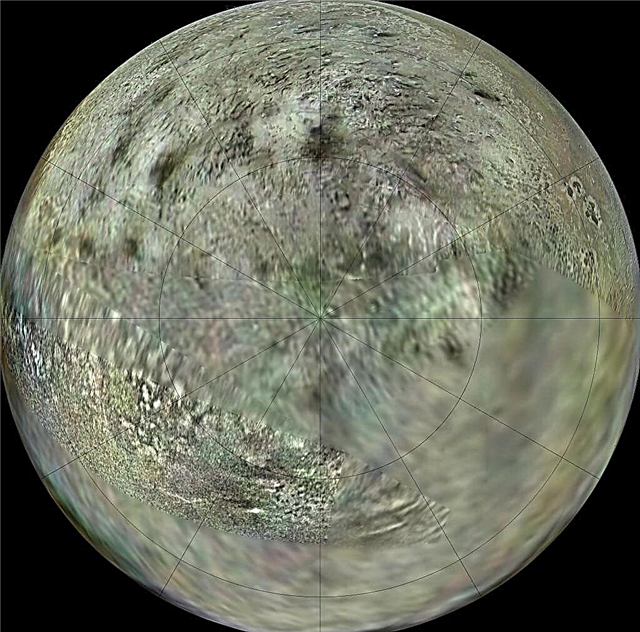
Kas olete mõelnud isegi sügavalt Buzz Lightyeari kuulsa sõnaühendi järele mänguasjaloost? Ilmselt mitte. Kuid võib-olla olete vahel vaatanud öist taevast ja mõelnud lõpmatuse enda olemuse üle.
Lõpmatus on veider mõiste, mõiste, mille järgi on inimese aju raske oma piiratud mõistmist ümbritseda. Me ütleme, et universum võib olla lõpmatu, kuid kas see võib tõesti jääda igaveseks? Või pi numbrid pärast koma - kas need kulgevad tegelikult lõputult, andes meile alati ringi täpsuse ja raadiuse suhte kohta palju suurema täpsuse? Ja kas Buzzil võib olla õigus? Kas on midagi lõpmatusest kaugemale?
Nende mõtlema panevate spekulatsioonide lahendamiseks värbas Live Science abi Philadelphia Pennsylvania ülikoolist pärit matemaatik Henry Towsnerilt, kes oli piisavalt lahke, et proovida vastata küsimusele "Kas oskate arvestada möödunud lõpmatusega?" (Ole hoiatatud: see läheb keeruliseks.)
Lõpmatus, Towsner ütles, istub võõras kohas: Enamik inimesi tunnevad, nagu oleks neil kontseptsioonist intuitsioon, kuid mida rohkem nad selle üle mõtlevad, seda veidramaks see muutub.
Ta lisas, et matemaatikud ei mõtle lõpmatusele sageli kui kontseptsioonile omaette. Pigem kasutavad nad selle mõtlemiseks erinevaid viise, et saada selle paljusid aspekte.
Näiteks on lõpmatus erineva suurusega. Seda tõestas Šotimaa St Andrewsi ülikoolist pärit ajaloo kohaselt saksa matemaatik Georg Cantor 1800. aastate lõpus.
Cantor teadis, et naturaalarvud - st terved positiivsed numbrid nagu 1, 4, 27, 56 ja 15 687 - jätkuvad igavesti. Need on lõpmatud ja nad on ka asjad, mida me kasutame asjade loendamiseks, seetõttu määratles ta neid kui karikatuuritegelase Charles Fisher Cooperi kasulikku ajalugu, matemaatikat ja muid teemasid käsitleva saidi kohaselt "loendamatult lõpmatu".
Vaieldamatult lõpmatute arvude rühmadel on mõned huvitavad omadused. Näiteks paarisarvud (2, 4, 6 jne) on samuti loendamatult lõpmatud. Ja kuigi neid on tehniliselt poole vähem kui neid, mida hõlmab täielik naturaalarvude komplekt, on nad ikkagi sama tüüpi lõpmatud.
Teisisõnu, võite paigutada kõik paarisarvud ja kõik naturaalarvud kõrvuti kahesse veergu ja mõlemad veerud lähevad lõpmatuseni, kuid need on lõpmatuse sama pikkusega. See tähendab, et pool loendatavast lõpmatusest on ikkagi lõpmatus.
Kuid Cantori suurepärane arusaam oli mõista, et on ka teisi numbrikomplekte, mis on loendamatult lõpmatud. Reaalarvud - mis hõlmavad nii naturaalarvu kui ka murdosasid ja irratsionaalseid numbreid nagu pi - on naturaalarvudest lõpmatumad. (Kui soovite teada, kuidas Cantor seda tegi ja saaksite hakkama mõne matemaatilise märkusega, siis vaadake seda Maine'i ülikooli töölehte.)
Kui joondada kõik naturaalarvud ja kõik reaalarvud kõrvuti kahte veergu, ulatuksid reaalarvud naturaalarvude lõpmatusest kaugemale. Cantor läks hiljem hulluks, arvatavasti põhjustel, mis ei olnud seotud tema tööga lõpmatuseni, Cooperi sõnul.
Mis on loendamine?
Niisiis, tagasi küsimuse juurde, kuidas arvestada mineviku lõpmatusega. "See, mille pärast matemaatika paneb küsima, on:" Mida see tegelikult tähendab? "Sõnas Towsner. "Mida sa mõtled, lugedes möödunud lõpmatust?"
Selle teemaga tutvumiseks rääkis Towsner järjenumbritest. Erinevalt kardinaalsetest arvudest (1, 2, 3 ja nii edasi), mis ütlevad teile, kui palju asju on komplektis, määratlevad ordinaadid nende positsioonide järgi (esimene, teine, kolmas jne) ja nad viisid nad matemaatikasse ka Kantor, matemaatika veebisaidi Wolfram MathWorld andmetel.
Järjekorranumbrites on mõiste omega, mida tähistatakse kreeka tähega ω, ütles Towsner. Sümbol ω on määratletud kui asi, mis tuleb pärast kõiki teisi naturaalarvu - või, nagu Cantor seda nimetas, esimene transfinite ordinaal.
Kuid üks numbrite kohta käivatest asjadest on see, et lõpus saate alati lisada veel ühe, ütles Towsner. Nii et on olemas selline asi nagu ω + 1 ja ω + 2 ja isegi ω + ω. (Juhul, kui olete mõelnud, lööd lõpuks numbri called1, mida nimetatakse esimeseks loendamatuks ordinaaliks.)
Ja kuna loendamine sarnaneb täiendavate numbrite lisamisega, võimaldavad need mõisted mingil moel lõpmatusest mööduda, ütles Towsner.
Selle kõige kummalisus on osa põhjustest, miks matemaatikud nõuavad oma terminite täpset määratlemist, lisas ta. Kui kõik pole korras, on meie normaalset inimese intuitsiooni raske lahutada matemaatiliselt tõestatavast.
"Matemaatika ütleb teile:" Vaatleme sügavalt, mis loeb? "Ütles Towsner.
Pelgalt surelike jaoks võib nende ideede täielik arvutamine olla keeruline. Kuidas täpselt tegelevad töötavad matemaatikud kogu selle naljaka ettevõtmisega oma igapäevases uurimistöös?
"Suur osa sellest on praktika," sõnas Towsner. "Te arendate kokkupuutel uusi intuitsioone ja kui intuitsioon ebaõnnestub, võite öelda:" Me räägime sellest täpsest täpsest rangest tõestusest. " Nii et kui see tõendusmaterjal on üllatav, saame ikkagi kontrollida, kas see on õige, ja siis õppida selle ümber uut intuitsiooni arendama. "